1.1 INTRODUCTION
A LA MICROSCOPIE A EFFET TUNNEL
En 1986, le prix Nobel de
Physique récompensa Gerd Binnig, Heinrich Rohrer et Ernst Ruska ; les deux premiers pour des travaux très récents,
le troisième pour des travaux vieux de plus de 50 ans! En exploitant le
principe de l’effet tunnel, Binnig et
Rohrer montrèrent en 1983 des images
à l’échelle atomique d’une surface de silicium balayée à l’aide d’une pointe
métallique [1,2]. Ruska, en 1931, avait réalisé le premier
microscope électronique. Deux découvertes prestigieuses, et deux principes
différents.
Jusqu’à la fin du siècle
dernier, les scientifiques pensaient atteindre l’observation de l’infiniment
petit en augmentant sans cesse le grandissement des microscopes optiques, tout
en réduisant les phénomènes perturbateurs. Le critère de Rayleigh
ruina tous leurs espoirs en établissant que la taille du plus petit détail
détectable ne peut être inférieure à la demi longueur d’onde l de la lumière utilisée. Parmi les trois
solutions classiques permettent d’augmenter la résolution : augmentation de
l’indice de propagation, augmentation de l’angle d’ouverture du système
collecteur et diminution de la longueur d’onde, la dernière fut retenue en utilisant
des rayonnements tels que les rayons X (Roentgen
en 1895) ou les rayons g. Sans grand succès!
Trente ans plus tard, les résultats de Louis de Broglie sur la dualité onde-corpuscule furent mis en
application par Busch (1927) afin de
produire des images en focalisant un faisceau d’électrons. Mais c’est à Ruska que reviendra la paternité du
premier microscope électronique, point de départ des générations de microscopes
à balayage (Oatley 1950) et à
transmission (Crewe 1968). Bien que
la résolution de tels microscopes ait formidablement augmentée (d’un facteur
100 par rapport à un microscope optique classique), ceux-ci travaillent
toujours dans un domaine que les opticiens nomment le « champ
lointain ».
En
optique, il a en effet été établi que le champ électromagnétique émis ou
réfléchi par un objet se compose de deux parties : une onde progressive et
une onde non radiative évanescente. Les hautes fréquences spatiales de l’objet
(supérieures à 2/l) produisent le champ
évanescent : si on veut accéder à ces informations fines, il faut donc
détecter les composantes non radiatives au voisinage immédiat de l’objet, à
l’aide d'une sonde. On travaille alors en « champ proche » et la
microscopie devient à « sonde locale », ce qui est le cas de la microscopie
STM.
Si l’invention du microscope
à effet tunnel est attribuée à Binnig
et Rohrer, on ne saurait oublier
toutes les tentatives réalisées antérieurement parmi lesquelles on peut citer
le topografiner de Young et al. Le
succès de Binnig et Rohrer est étroitement lié aux
formidables progrès réalisés en électronique, permettant notamment le balayage
à des distances très proches de la surface (de l’ordre du nanomètre) mais aussi
la détection et la régulation de courants électriques d’intensité aussi faible
que le nanoampère.
Avant de développer en
détail le principe de l’effet tunnel, quelques notions sur la microscopie
tunnel doivent être rappelées.
1.2 LE MICROSCOPE A EFFET TUNNEL
Le microscope à effet tunnel
est un microscope à balayage mesurant un courant tunnel It résultant
de l’application d’une différence de potentiel V entre une pointe métallique et
une surface conductrice. Des surfaces métalliques ou semi-conductrices sont
ainsi observées sur des zones allant du micromètre à la fraction du nanomètre,
c’est-à-dire à l’échelle atomique. Dans nos expériences, nous avons utilisé un
microscope STM/AFM sous ultravide de marque OMICRON. L’échantillon est placé
sur un tube piézo-électrique autorisant des déplacements dans les trois directions,
avec des résolutions latérales de 1/10ièmeÅ
et une résolution verticale (en Z) de 1/100ièmeÅ permettant
d’obtenir la résolution atomique.
La figure 1.1 présente une photographie du microscope utilisé :
Figure 1.1 : Photographie du microscope
STM.
Ce microscope est suspendu à
quatre ressorts. En position abaissée, un système d'amortissement par courants
de Foucault isole le microscope des perturbations vibratoires extérieures.
1.2.2) Le
principe de fonctionnement du microscope
Le microscope permet de balayer la surface suivant
différents modes de fonctionnement :
·
à hauteur Z(It) constante,
·
à courant It(Z) constant,
·
et en mode spectroscopique (mesure de It(V)).
Dans son
mode le plus couramment utilisé, l’électronique permet de produire des images à
courant constant ; le courant tunnel mesuré en chaque point de la surface est
comparé à un courant de référence Iréf fixé par l’utilisateur. Une
boucle de régulation ajuste, via le tube piézo-électrique, la distance pointe-surface
afin de conserver le courant tunnel égal à Iréf. Lorsque It >Iréf,
la distance augmente. Elle diminue dans le cas contraire. La conversion de la
tension appliquée au tube piézo-électrique dans une échelle de couleurs donne
une image STM. Toutes les informations sont ensuite traitées par un ordinateur.
Remarquons que le fonctionnement d’un tel microscope impose l’utilisation d’une
électronique performante capable de mesurer des intensités de courant de
quelques pico-ampères.
La figure 1.2 présente
de manière succincte le fonctionnement du microscope :
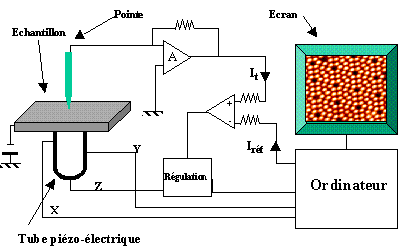
Figure 1.2 : Schéma fonctionnel du
microscope à effet tunnel.
Ce microscope offre donc la
possibilité d’observer des surfaces métalliques ou semi-conductrices via la
mesure d’un courant tunnel. Pour interpréter correctement les informations
incluses dans une image STM, nous allons maintenant établir l’origine physique
de l’effet tunnel.
1.3 LE PRINCIPE DE L’EFFET TUNNEL
En mécanique
classique, un électron, rencontrant une barrière de potentiel, ne peut la
traverser s’il possède une énergie E inférieure à celle de la barrière. Dans
une approche quantique, la fonction d’onde y associée à l’électron n’est
pas nulle à l’intérieur et au-delà de la
barrière de potentiel. Dans ces conditions, les électrons ont la
possibilité de franchir la barrière de potentiel lorsque la largeur de
celle-ci n’est pas trop grande : c’est ce qu’on appelle l’effet tunnel.
1.3.1) Première approche avec un modèle
unidimensionnel
Considérons
le modèle unidimensionnel (figure 1.3)
où un électron incident, auquel est associée une onde YG, rencontre une barrière de
potentiel U(z) de largeur d. Dans le cadre de la théorie quantique, les
solutions de l’équation de Schrödinger pour chaque région correspondent à deux
ondes progressives YG et YD à gauche et à droite de la
barrière, et à une onde évanescente à l’intérieur de la barrière [3].
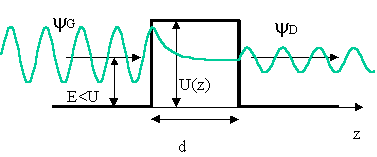
Figure 1.3 : Barrière de potentiel dans
un modèle unidimensionnel.
A
l’aide des conditions de continuité, on établit l’expression du
coefficient de transmission T(E) d’un électron de la partie gauche de la
barrière vers la droite:
(1.1)
Dans
le cas d’une barrière de potentiel de forme quelconque et dans l’approximation Wentzel-Kramers-Brillouin (WKB), T(E)
s’écrit [4]:
(1.2)
Pour
fixer quelques grandeurs relatives à la microscopie STM, considérons une
barrière de potentiel U = 4 eV (valeur typique rencontrée dans le cas d’un
métal) de largeur d = 1 nm. Pour un électron d’énergie E = 2 eV, la longueur de
décroissance l à l’intérieur de la
barrière de potentiel U, définie par l =
É/Ö(2m(U-E)), vaut environ 0,14
nm. D’après la relation 1.1, le
coefficient de transmission est de l’ordre de 10-6. Lorsqu’on
augmente de 0,2 nm la largeur de la barrière, T(E) décroît d’environ un facteur
10, conséquence de la décroissance exponentielle du coefficient de
transmission.
Dans
une première approche du fonctionnement d’un microscope à effet tunnel, on
considère généralement deux électrodes polarisées, de travaux de sortie FG et FD, séparées par un isolant
(par exemple le vide). Les niveaux de Fermi EFG et EFD
des deux électrodes se décalent en fonction de la différence de potentiel
électrique appliquée V et un courant tunnel s’établit à travers la barrière de
potentiel.
Lorsqu’on applique une
faible tension entre les deux électrodes (½eV½ << F), la barrière de potentiel peut être
modélisée par une forme trapézoïdale (figure
1.4).
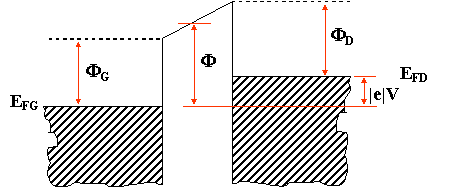
Figure 1.4 : Barrière de potentiel
trapézoïdale, EFG et EFD
correspondent aux niveaux de
Fermi des électrodes.
On
peut démontrer que, dans ces conditions, le courant tunnel s’écrit de la
manière suivante [5] :
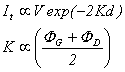(1.3)
Dans
cette expression 1.3, uniquement
valable dans le cas des électrons libres et pour une faible tension V
appliquée, le courant tunnel est
directement proportionnel à la différence de potentiel V et dépend
exponentiellement de la distance entre les deux électrodes.
1.3.2) Courant tunnel dans une approche
hamiltonienne
Dans cette approche plus
réaliste, on considère que le faible recouvrement des orbitales atomiques des
deux électrodes est à l’origine du courant tunnel.
La figure 1.5 présente le diagramme d’énergie du système comprenant
les deux électrodes séparées par le vide. Les énergies sont référencées par
rapport au vide.
Lorsqu’on approche les deux
électrodes et qu’elles ne sont plus séparées que de quelques angströms,
l’énergie potentielle UB de la barrière est différente des énergies
UG et UD des électrodes de gauche et de droite
lorsqu’elles sont isolées.
Afin de pouvoir mettre en
œuvre la méthode des perturbations dépendantes du temps, on a coutume de
séparer le système en deux sous-systèmes, de part et d’autre de z = 0. On
identifie alors :
·
UG
avec UB pour z < 0 (en prenant UD = 0)
·
et
UD avec UB pour z > 0 (en prenant UG = 0).
La différence des niveaux
d’énergie entre les deux électrodes vérifie : EFG-EFD
= eV.
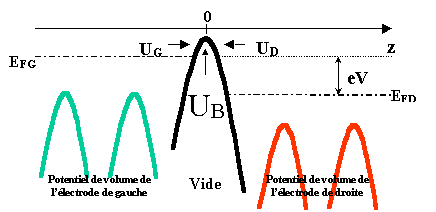
Figure 1.5 : Diagramme des énergies d’un
système à deux électrodes séparées par du vide.
D’après
les travaux de Lang [6,7], basés sur le formalisme
hamiltonien tunnel de Bardeen [8], à chaque électrode est associé un
hamiltonien noté HG (respectivement HD) vérifiant :
(1.4)
La fonction d’onde d’un
électron tunnel peut s’écrire comme une combinaison linéaire des états des deux
électrodes :
Y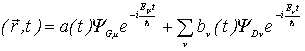
(1.5)
avec 
(1.6)
où m et n réfèrent respectivement les états
électroniques des électrodes de gauche et de droite. A t = -¥, l’électron est dans l’état FGm avec les conditions aux
limites : a(-¥) = 1 et bn(-¥) = 0 [9,10].
Lorsqu’on
rapproche les deux électrodes, l’Hamiltonien total s’écrit H = HG+UD.
En considérant l’interaction entre les deux électrodes comme faible, la
résolution de l’équation de Schrödinger dépendante du temps dans la théorie des
perturbations au premier ordre, nous amène à définir la matrice de transition Mmn d’un électron de l’état m de gauche vers l’état n de droite:
(1.7)
en
utilisant le théorème de Green, on peut réécrire 1.7 :
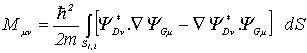(1.8)
où
l’on intègre 1.8 sur une surface
dans la barrière de potentiel entre les deux électrodes. D’après la règle d’or
de Fermi, l’expression du courant tunnel, en fonction de la différence de
potentiel V, de la matrice de transition Mmn et de la fonction de
distribution de Fermi-Dirac f , est:
soit :
(1.9)
avec :
Pmn représentant la probabilité
de transition de l’électron de l’état m vers l’état n.
Dans la limite des faibles
tensions et températures, l’expression du courant tunnel devient :
(1.10)
Le principal
problème revient à évaluer la matrice de transition en fonction de l’expression
analytique des états des deux électrodes. Pour mieux rendre compte du
fonctionnement du microscope, l’une des électrodes est remplacée par une
pointe : la mesure du courant tunnel devient ainsi locale. Même si les
théories actuelles permettent de décrire correctement les fonctions d’onde
associées aux états électroniques de la surface, la modélisation d’une pointe
réelle est complexe.
1.3.3) Modélisation d’une pointe
C’est à Tersoff et Hamann [11-14] que
l’on doit les premiers calculs d’image tunnel sur les reconstructions de la
surface Au(110), à partir de considérations simples sur la géométrie de la
pointe et la forme des fonctions d’onde en présence.
Dans
leurs travaux, la pointe est modélisée par un puits de potentiel sphérique
(orbitale atomique s). La fonction d’onde Ym associée à la pointe
s’écrit sous la forme :
Y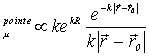
(1.11)
Sur la figure 1.6, l'extrémité de la pointe est représentée comme une
sphère de rayon R centrée en 
.
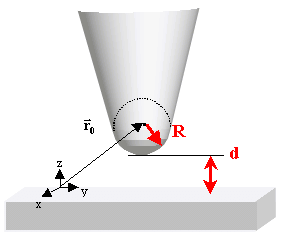
Figure 1.6 : Géométrie d’une pointe d’après Tersoff et Hamann.
Les
fonctions d’onde des états électroniques yn associées à l’échantillon de
surface sont développées sous la forme :
Y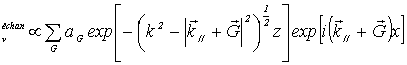
(1.12)
où k = Ö(2mF/h2), F représente le travail de sortie des
électrons (considéré comme étant le même pour la surface et la pointe), 
est un vecteur d’onde de Bloch et 
un vecteur du réseau
réciproque de la surface. Ces fonctions d’ondes sont périodiques dans le plan
de la surface et décroissantes dans le vide. A partir de ces définitions de Ym et Yn, l’expression analytique de
la matrice de transition Mmn peut être calculée
simplement. On en déduit l’expression
du courant tunnel suivante :
(1.13)
Cette
relation montre que I est proportionnel à la densité d'états de la pointe Dpointe(EF)
et à la densité d’états locale de la surface r(
,EF) à la position 
de la pointe et au
niveau de Fermi. Les images STM
représentent donc une mesure locale des courbes d’isodensités d’états. Il
convient de prendre en compte l’influence de cette densité d’états dans
l’interprétation des images. De plus, cette théorie montre que la résolution
latérale ne dépend que la forme de la pointe. Dans la référence [11], Tersoff définit cette résolution latérale et l’exprime, tous
calculs faits, sous la forme final simple : (2(R+d))1 /2
où cette expression, R et d sont exprimés en angströms.
Pourtant,
même si la théorie de Tersoff et Hamann permet de comprendre les images
en microscopie à effet tunnel, elle n’explique pas toutes les observations
expérimentales, comme l’origine de la résolution atomique. Lorsque la distance
pointe-échantillon est faible, l’interaction forte entre la pointe et la
surface doit être prise en compte, ce qu’ont fait W. Sacks et C. Noguera [15,16]. Dans ce cas, la théorie de Bardeen n’est plus valable.
Chen et al. ont montré, dans un modèle
unidimensionnel, que la rugosité (définie comme la différence de hauteur Zmax-Zmin)
augmente en tenant compte des orbitales p et d [17]. En utilisant une chaîne linéaire dans le sens de déplacement
x de la pointe, les matrices de transition
avec des orbitales s, p et d peuvent être déterminées simplement. Les
rapports de rugosité s’écrivent :
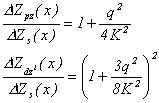(1.14)
avec K
= Ö(2mF)/h et q = 2p/a où F représente le travail de
sortie des électrons et a est le paramètre de maille. Pour F = 4 eV, K »1 Å-1 et avec a =
4 Å, on remarque que la rugosité augmente d’un facteur 1,6 pour une orbitale pz
et de 3,7 pour une orbitale dz2. Il convient donc d’introduire des
modélisations plus réalistes de la pointe pour décrire correctement les
observations STM du point de vue théorique.
1.3.4) Les images en microscopie à effet
tunnel
En fonction de la différence de potentiel V entre
l’échantillon et la pointe (le potentiel de la pointe est pris comme
référence), les images STM peuvent être considérablement modifiées. En
effet, en microscopie à effet tunnel, les images représentent une cartographie
des courbes d’isodensités d’états au niveau de Fermi (comme l’indique l’équation
1.13). La figure 1.7 illustre l’influence de la différence de potentiel sur
le courant tunnel.
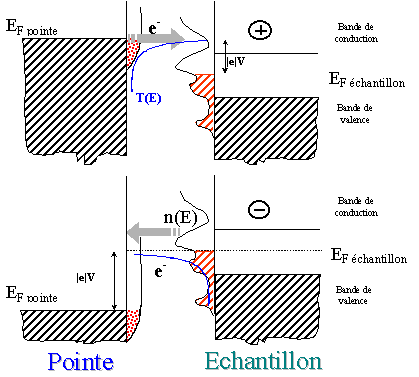
Figure 1.7 : Contribution au courant tunnel en fonction de la polarité et de la
tension.
D’après l’expression du
coefficient T(E) (relation 1.1),
plus l’énergie des électrons est importante, plus la probabilité de
transmission est grande. Dans ces conditions, les électrons contribuant au
courant tunnel proviennent essentiellement du niveau de Fermi. Notons que la
densité d’états de la pointe métallique peut être généralement considérée comme
constante.
En
polarité positive, les électrons tunnel traversent la barrière de potentiel de
la pointe vers les états vides de la densité d’états n(E) de l’échantillon.
Ainsi, une variation de tension permet de sonder les états vides de la surface.
En
polarité négative, les électrons contribuant au courant tunnel proviennent du
niveau de Fermi de la surface de l’échantillon. Dans ce cas, l’image devient peu
sensible à la densité d’états pleins de la surface.
L’amplitude des effets spectroscopiques est en général très
faible (quelques Angströms) et ne se rencontre que dans le cas d’observation en
résolution atomique ou lorsque la rugosité est faible. Il est alors nécessaire
d’observer la surface pour des valeurs de la tension différentes afin de
dissocier, si possible, la topographie des effets spectroscopiques.
La
pointe, lors d’un expérience de microscopie STM, est un élément crucial et
difficilement contrôlable dans le temps. Dans ce paragraphe, nous allons
décrire la méthode de préparation utilisée dans notre laboratoire. Les pointes de tungstène
sont préparées en deux étapes.
La première étape consiste en une attaque électrochimique à l’aide d’une solution de NaOH. Cette technique permet de fabriquer, de manière reproductible, des pointes extrêmement fines avec des rayons de courbure, dans le meilleur des cas, de l’ordre de 5 à 10 nm [18].
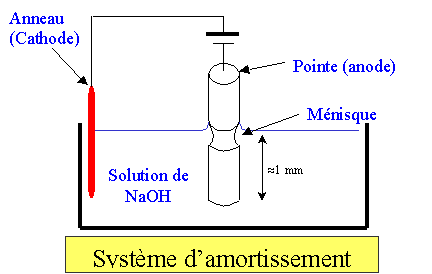
Figure 1.8 : Dispositif de fabrication
des pointes STM.
L’extrémité
du fil de tungstène est plongée dans la solution de NaOH (figure 1.8) avec une concentration de 2 moles/litre ; une
tension continue d’environ 12 Volts est appliquée entre les deux électrodes
pour activer la réaction chimique. Les ions OH- étant consommés lors
de la réaction, la solution de NaOH n’est utilisée que pour quelques pointes.
Lors du processus, le fil de tungstène se dissout en oxyde de tungstène au
niveau du ménisque (jusqu’à la rupture du fil en deux) suivant la
réaction :
En mode DC, l’attaque
électrochimique continue après la rupture du fil. Il est donc nécessaire de
stopper la réaction dès cette rupture, pour conserver une pointe fine. Le
dispositif électronique, présenté en figure
1.9, permet d’effectuer cet arrêt.
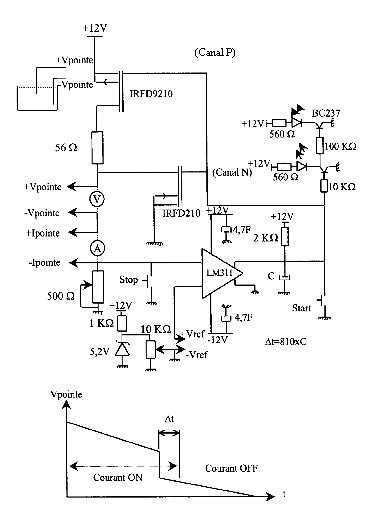
Figure 1.9 : Dispositif électronique utilisé pour arrêter
la réaction chimique (d’après un circuit du Naval Research
Lab - 1990).
Le diamètre du fil de tungstène
diminuant sous l’effet de la réaction, il s’ensuit une diminution de la différence de potentiel entre la pointe
et l’entrée + du comparateur. Cette dernière est comparée à une tension Vréf
afin d’arrêter le processus. La tension Vréf choisie correspond à la
tension de rupture du fil. Notons que, la réaction s’effectuant dans le
ménisque, il est très important d’éviter toute vibration lors de l’attaque
électrochimique.
La figure 1.10
présente une image obtenue au microscope électronique à balayage d’une pointe
STM en tungstène (diamètre du fil : 0,35 mm) réalisée suivant la méthode
décrite précédemment avec une tension Vréf = 300 mV.
Figure 1.10 : Image de pointe STM obtenue par
microscopie à balayage électronique.
La deuxième étape consiste à
chauffer la pointe sous ultravide par bombardement électronique. La température
à l’extrémité de la pointe est difficilement contrôlable. Cependant elle est
suffisante pour éliminer les sels de soude restants de l’attaque électrochimique
et induire une réorganisation de l'extrémité de la pointe. Un chauffage à plus
haute température est possible mais risquerait d’arrondir la pointe.
Lors de nos expériences en microscopie, aucun dépôt de matière n’est observé lors de l’approche et durant le balayage de la surface ; de plus, la résolution atomique est systématiquement obtenue sur la surface du substrat et des siliciures. Ces deux critères sont suffisants pour considérer cette technique de fabrication comme adaptée à nos besoins.
1.5 LE DISPOSITIF EXPERIMENTAL
L’ensemble
des expériences a été réalisé dans une enceinte sous ultravide (figure 1.11) avec une pression dans la
gamme de 10-11 mbar afin d’éviter toute contamination (oxygène,
carbone, hydrogène,…) pouvant perturber les analyses. Cette enceinte se compose
d’une seule chambre permettant de préparer les pointes et les échantillons. Un
bras xyzq, une canne de transfert et
un manipulateur permettent de déplacer les échantillons du sas d’entrée rapide
vers la chambre et les différents appareils d’analyse.
Figure 1.11 : L’enceinte UHV et ses
équipements.
Pour enlever la couche
d’oxyde et reconstruire les surfaces, les échantillons, chauffés par effet
Joule, sont placés sur un porte-échantillon solidaire du bras xyzq. Le bras permet de
positionner les échantillons devant les évaporateurs, les dispositifs d’analyse
en Diffraction d’Electrons Lents (DEL) et de Spectroscopie d’Electrons Auger,
le canon à ions ou le pyromètre optique. L’appareil d’analyse DEL est
particulièrement utile pour identifier les reconstructions de surface.
1.6 TECHNIQUES DE PHOTOEMISSION UV ET DE SPECTROSCOPIE DE DIFFUSION
D'IONS
Une
équipe de recherche du Laboratoire de Physique et de Spectroscopie Electronique
de Mulhouse (L.P.S.E. UPRES A N°7014) s’est spécialisée dans l’étude des
systèmes terres rares/silicium. Leurs résultats obtenus par diverses techniques
d'analyse de surface, confrontés à nos résultats STM sur le siliciure d’erbium,
ont permis une collaboration fructueuse. Dans ce contexte, une partie de mon
travail (interface Er/Si-B) a pu être
réalisée au sein de l’équipe du Professeur Gewinner du L.P.S.E. pour
caractériser les dépôts en photoémission UV et en spectroscopie de diffusion
d’ions ISS. Ce paragraphe présente succinctement ces deux techniques
d’investigation.
1.6.1) Introduction aux techniques de
photoémission
L’explication
de l’effet photoélectrique en 1905 par Einstein
est à l’origine des diverses techniques de photoémission s’appuyant sur
les théories d’interactions rayonnement-matière; pourtant, celles-ci ne sont
apparues que dans les années 1970 et valurent à Kai Siegbahn le prix Nobel de Physique (1981) pour sa contribution
à l’élaboration de l’ESCA (Electron Spectroscopy for Chemical Analysis)
regroupant diverses techniques de photoémission telles l’UPS et l’XPS.
La photoémission
XPS (X-ray Photoemission Spectroscopy) ou UPS (Ultraviolet Photoemission
Spectroscopy) sont des techniques d’analyse de surfaces et d'interfaces très
utilisées. Toutefois, elles ne permettent de sonder que les états électroniques
occupés du solide, que ce soient des états de volume ou de surface (la
photoémission inverse permet de sonder les états vides). Alors que la
microscopie STM
nous donne des images locales des surfaces (topographie et spectroscopie) dans
l’espace réel, la photoémission UV détermine la population électronique moyenne
dans l’espace réciproque.
Pour ces
expériences, diverses sources de photons sont disponibles. Il est pourtant nécessaire de
choisir convenablement la source de rayonnement pour extraire les électrons
porteurs de l’information recherchée. En photoémission UV, on utilise un
rayonnement ultraviolet issu de la désexcitation de l’hélium ou du néon (HeI : hn = 21,2 eV et NeI :
hn = 16,8 eV) pour
sonder les états dont l’énergie est de l’ordre de 0 à 20 eV sous le niveau de
Fermi, avec en particulier ceux de la bande de valence. En irradiant
l’échantillon avec des photons dont l’énergie est dans le domaine des rayons X
(XPS) (par exemple une source Mg : Ka = 1253,6 eV), nous avons de plus accès aux niveaux de cœur
des atomes.
L’autre élément important d’un spectromètre est l’analyseur. Celui-ci utilise un champ électrique agissant sur la trajectoire des électrons. L’analyseur présente une conception hémisphérique permettant aux électrons, après une déflexion de 180°, d’être détectés et amplifiés par un channeltron. Selon l’angle solide dans lequel les photoélectrons sont collectés par l’analyseur, la photoémission UPS est dite angulaire ou intégrée. Dans notre cas, l’analyseur collecte les photoélectrons dans un angle solide dont l’ouverture est de ±1° autour de la direction q, ce qui permet de mesurer à la fois l’énergie des photoélectrons et leur position dans la zone de Brillouin. De ce fait, cette technique constitue une sonde quasi-ponctuelle dans l’espace réciproque. Nous montrerons dans le paragraphe suivant que ce type de mesure permet en particulier de remonter à l’énergie des états occupés en chaque point de la zone de Brillouin. Elle permet donc de déterminer la structure de bandes expérimentale d’un cristal.
1.6.2) La photoémission UV angulaire
(ARUPS)
La figure 1.12 présente la géométrie d’une
expérience de photoémission et les paramètres généralement utilisés.
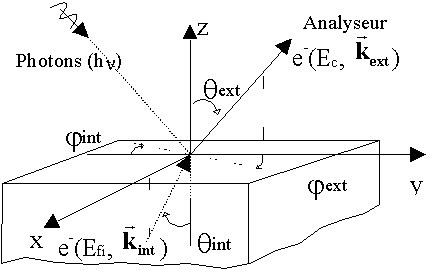
Figure 1.12 : Géométrie de
l’expérience UPS.
La surface est éclairée par
un rayonnement ultraviolet d’énergie hn. Dans
le matériau, un électron est excité d’un état occupé Ei(
) vers un état vide Efi(
) (figure 1.13a),puis
se propage vers la surface suivant une direction qint et jint [19,20]. Lorsque l’énergie hn du photon est supérieure à la barrière de potentiel F représentant le travail d’extraction
d’un électron du solide, cet électron peut être extrait de la matière avec une
énergie cinétique EC (figure
1.13b). Il est ensuite collecté suivant une direction
caractérisée par les angles qext et jext. Un analyseur
hémisphérique
permet de comptabiliser le nombre d’électrons par niveau d’énergie : on
obtient ainsi un spectre de photoémission (figure
1.13c) traduisant la probabilité de présence
d’électrons ayant une énergie de liaison (EF-Ei).
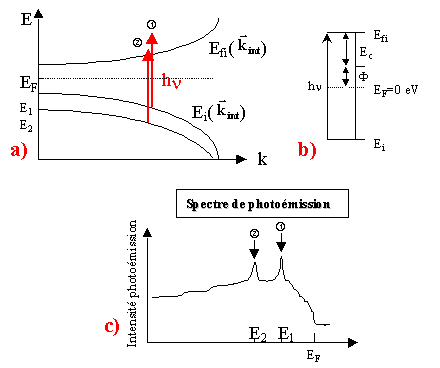
Figure 1.13 : (a) principe
d’excitation d’un électron par un photon, (b) diagramme de conservation de
l’énergie, (c) spectre de photoémission.
L’énergie
cinétique étant liée à l’énergie de liaison des électrons, on obtient un pic à
la position Ei sur le spectre de photoémission (figure 1.13c).
De ce
fait, l’évolution de l’énergie de liaison des états associés aux différents
pics sur les spectres de photoémission, en fonction de l’angle qext, permet de déterminer la
structure électronique des états pleins, caractéristique du solide cristallin
dans l'espace réciproque.
Toutefois, dans l’analyse
des résultats, il faut pouvoir dissocier les émissions provenant du volume et
celles provenant de la surface, ce qui est généralement délicat. La périodicité
tridimensionnelle du volume étant brisée par la surface, celle-ci introduit de
nouveaux états électroniques appelés états de surface, localisés dans la bande
interdite de la structure électronique du volume ou bien en bords de bandes de
volume. On peut grossièrement distinguer deux types d’états :
·
les
résonances de surface qui sont issues des états de volume par modification du
potentiel cristallin et qui sont situées en bords de bandes de volume
·
et
les états de surface vrais, situés dans les bandes interdites de la structure
de bandes de volume.
Pour différencier les états
de volume de ceux de surface, il faut tenir compte de leurs caractéristiques,
dont quelques éléments sont donnés ici :
·
ils
sont généralement plus sensibles à l’adsorption d’éléments étrangers que ceux
de volume. Ceci n’est pas toujours le cas et ce critère seul ne suffit pas.
·
les
ondes électroniques associées aux états de surface se propagent parallèlement à
la surface. Ces états ont une énergie indépendante de la composante du vecteur
d’onde 
perpendiculaire à la
surface. La grandeur 
étant conservée, la
courbe de dispersion Ei(
) doit être indépendante de l’énergie des photons.
Nous pouvons
formuler simplement les relations liant l’énergie de liaison Ei et
le vecteur d’onde 
. Dans l’approximation à un électron, le principe de
conservation de l’énergie permet de décrire le processus d’excitation d’un
électron par un photon à l’intérieur du solide :
(1.15)
Soit F le travail
d’extraction. L’énergie cinétique Ec(
) d’un électron extrait de la surface est (figure 1.13c):
(1.16)
soit 
(1.17)
La
surface influence seulement la composante du vecteur d’onde 
perpendiculaire à la
surface. Les angles jext et jint sont égaux et la composante
parallèle 
est conservée, ce qui
implique 
=
. On en déduit les relations suivantes :
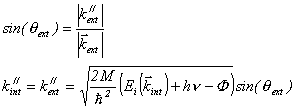(1.18)
La
mesure de Ec, pour une valeur de qext donnée, nous permet de
remonter à la
valeur de Ei(
). Ce type d’expérience ne donne pas accès seulement à
l’énergie initiale d’un électron mais aussi au vecteur d’onde 
correspondant. Ainsi, en mesurant Ec pour chaque
angle, les relations 1.18 nous
permettent de tracer la courbe de dispersion Ei(
) décrivant l’évolution des états électroniques dans le
réseau réciproque.
1.6.3) La spectroscopie de diffusion d’ions
de basse énergie ISS
Alors
que la photoémission UV extrait des électrons de la surface via une interaction
rayonnement-matière, la spectroscopie ISS consiste à produire des collisions
ions-surface [21]. La surface est
bombardée par un faisceau d’ions monocinétiques de masse Mi. La
mesure de l’énergie cinétique des ions diffusés par
la surface permet de déterminer la nature chimique des atomes de surface. La figure 1.14 représente schématiquement
le processus de l’interaction ion-surface.
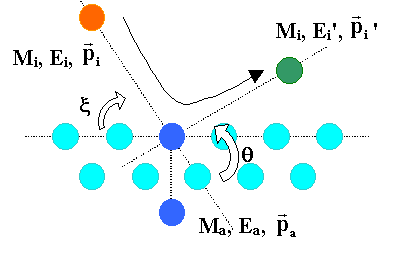
Figure 1.14 : Schéma de l’interaction
ion-surface.
Dans
ce type d’expérience, un atome de surface est considéré comme isolé et
l’équation régissant l’interaction peut être décrite par la mécanique
classique. De ce fait, un ion incident de masse Mi, d’énergie Ei
et de quantité de mouvement 
interagissant avec la
surface sous l’angle x est dévié après la
collision. L’atome de surface acquiert une énergie Ea et une
quantité de mouvement 
alors que l’ion
rétrodiffusé voit son énergie et sa quantité de mouvement modifiées.
En
écrivant les lois fondamentales de conservation de l’énergie et de la quantité
de mouvement, on peut établir la relation 1.19
reliant l’énergie des ions diffusés et la masse des éléments chimiques présents
en surface dans une direction de détection
donnée par l’angle q :
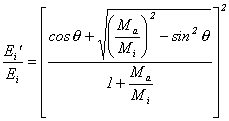(1.19)
Expérimentalement, les ions incidents
sont des ions He+ ce qui permet de mesurer les masses Ma
de tous les atomes à partir du lithium. On obtient ainsi un spectre ISS, comme
celui de la figure 1.15, présentant des
pics à certaines énergies, spécifiques de la masse des diffuseurs et de l’angle
q sous lequel sont collectés les ions
diffusés.
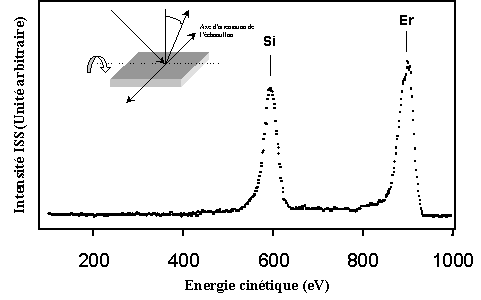
Figure 1.15 : Spectre ISS
pour une direction donné dans le cas du siliciure d'erbium.
Si on connaît Ei, Mi et q, la mesure de Ei' permet de déterminer Ma. Ainsi
la position énergétique des pics dans le spectre ISS révèle la nature chimique
des atomes présents sur la surface.
En
seulement une vingtaine d’années d’existence, la microscopie en champ proche
STM a su s’imposer parmi les principales techniques d’investigation des
surfaces. L’arrivée de cet instrument d’analyse a modifié complètement la
connaissance des surfaces en offrant des images locales de la topographie et de la spectroscopie avec une
résolution pouvant atteindre l’échelle atomique. Dans des conditions
d’ultravide, les images en résolution atomique ont permis de mieux comprendre
les mécanismes de reconstruction des surfaces et de croissance, de mesurer localement
le comportement électronique, et de confirmer des modèles structuraux obtenus
par des techniques non locales.
La
capacité d’obtenir des images locales permet aussi d’observer des structures
non détectables avec d’autres techniques d’analyses et donc de mieux comprendre
les mécanismes de formation d’une interface. Les informations sur la
morphologie de la surface, sur ses propriétés électroniques et sur sa nature
chimique, obtenues respectivement à l’aide de la microscopie STM, de la
photoémission UV et de la spectroscopie ISS, donnent ainsi une
« image » très complète de l’interface étudiée.
Remarquons
que, contrairement aux techniques de photoémission qui analysent sur des
surfaces d’environ 1 cm2, la microscopie en champ proche STM apporte
des informations concernant des surfaces de quelques mm2 au maximum. De ce fait, compte
tenu des éventuelles inhomogénéités dues à la température de recuit et au
dépôt, de nombreuses expériences sont nécessaires pour s’assurer que les images
sont bien représentatives du comportement global de l’interface.
Références bibliographiques
du chapitre 1:
[1] G. Binnig, H. Rohrer, Ch. Gerber, E. Weibel, Phys.
Rev. Lett. 49, 57 (1982)
[2] G. Binnig, H. Rohrer, Ch. Gerber, E. Weibel, Phys.
Rev. Lett. 50, 120 (1983)
[3] C. Cohen-Tannoudji, B. Diu, F.
Laloë, « Mécanique Quantique I », Edition Hermann
[4] R. Holm, B. Kirschstein, Z. Tech. Physik
16, 488 (1935)
[5] J.G. Simmons, J. Appl. Phys. 34, 1793 (1963)
[6] N.D. Lang, Phys. Rev. Lett. 55, 230 (1985)
[7] N.D. Lang, Phys. Rev. B, 34, 5947 (1986)
[8] J. Bardeen, Phys. Rev. Lett. 6, 57 (1961)
[9] M.C. Desjonquères, D. Spanjaard,
« Concept in surface physics », Springer-Verlag, Surface Sciences 30
[10] R. Wiesendanger, H.J. Güntherodt,
« Scanning tunneling microscopy III », Springer-Verlag, Surface
Sciences 29
[11] J. Tersoff, D. R. Hamann, Phys. Rev.
Lett. 50, 1998 (1983)
[12] J. Tersoff, Phys. Rev. B, 40, 11990 (1989)
[13] J. Tersoff, Phys. Rev. B, 41, 1235 (1990)
[14] J. Tersoff, Phys. Rev. B, 39, 1052 (1989)
[15] W. Sacks, C.
Noguera, J. Vac. Sci. Technol. B9(2), 488 (1991)
[16] W. Sacks, C.
Noguera, Phys. Rev. B, 43, 11612 (1991)
[17] C. J. Chen, Phys. Rev. B42, 8841 (1990)
[18] B.
Grandidier, Thèse de doctorat, « Contribution à l’étude de faces clivées
(110) de semi-conducteurs III-V par spectroscopie STM en UHV : Application
au dopage planaire de silicium dans GaAs », Université des sciences et
techniques de Lille Flandres-Artois (1997)
[19] G.V. Hansson, R.I.G. Uhrberg, Surf. Sci. Reports
9, 197 (1988)
[20] E.W. Plummer, W. Eberhardt,
« Angle-resolved photoemission as a tool for the study of surfaces »,
533-649
[21] J. Grimblot,
« L’analyse de surface des solides par spectroscopies électroniques et
ioniques », Collection Mesures Physiques, Edition Masson